Julia package development workflow
In an effort to make a better MARS package and learn Julia, I’ve been making a MARS package in Julia. I had a hard time figuring out how to set up my development environment and workflow. What software do I need? How do I configure it? Where do I put stuff? How do I run my tests? This post is about my answers to those questions. I’m using Mac OS 10.9.5.
Software installation
I’m using Juno to edit my Julia files. Installation is pretty easy.
Install the latest Julia and Juno from the download site.
- You then have to tell Juno where to find Julia. I guess it comes bundled with its own Julia, which will only lead to problems. See the docs for more details on this:
- Start Juno.
- Press Ctrl-Space.
- Type “Settings: User behaviors” and press Enter.
- Add [:app :lt.objs.langs.julia/julia-path “/path/to/julia”] to the settings file that appears, where “path/to/julia” is replaced with the path to the Julia you just installed. In my case, the path is “/Applications/Julia-0.3.10.app/Contents/Resources/julia/bin/julia”.
Project setup
Julia projects are easy to set up if you just want to write scripts or interact with IJulia. Writing packages is a little trickier. Here are steps to get you started.
- From Juno,
- Type Ctrl-Space.
- Type “spawn” and press Enter.
- From the spawned Julia terminal,
- Type Pkg.generate(“MyPackage”, “MIT”). Here “MyPackage” is the name of your package and “MIT” is the desired license. If you don’t like the license, you can change it later.
Julia generated a skeleton for your new package and put it somewhere in your .julia directory. It kind of sucks having to work with your code in some hidden configuration directory, so move the created package to wherever you like and then create a symbolic link from .julia. Julia won’t know the difference. Also, rename it with a ”.jl” extension. In the terminal, do:
mv ~/.julia/v0.3/MyPackage workspace/MyPackage.jl
ln -s workspace/MyPackage.jl ~/.julia/v0.3/MyPackage
Your Julia version might be different, so check that.
- Open your package in Juno. Go to File->Open folder and select MyPackage from your workspace.
Development cycle
Julia automatically created src and test directories, as well as src/MyPackage.jl and test/runtests.jl. To work on your package, do the following:
- Edit your code.
- Edit your tests.
- Make sure runtests.jl runs all your tests. People usually use include() or just write all the tests directly in the file.
- From your spawned julia terminal, do Pkg.test(“MyPackage”).
- GOTO 1.
Version control and publishing
The package directory created by Julia is already a git repository. You can add it to github if you want. I haven’t published any packages yet, but see the Julia manual for information on how to do it.
How to sample from a hazard function
When you develop new methods, it’s important to test them on simulated data. Recently I’ve been developing some survival analysis methods and found myself needing to simulate survival data sets with arbitrary hazard functions. I searched and searched and couldn’t find a good way to do it, so I thought I’d share my solution here.
Still alive?
Survival analysis is the part of statistics that deals with waiting. It is named for that special kind of waiting in which we all must participate, but it is applicable to any kind of waiting for something to happen. I like to use it at the airport, for example. The core object in survival analysis is the survival function, which gives the probability that you will still be waiting (e.g., still alive) as a function of time. The hazard function is the negative time derivative of the survival function normalized by the survival function,
or, more intuitively, it is the instantaneous rate at which events (such as death) occur among the remaining survivors.
Sampling from the hazard function means drawing random numbers from the distribution that that hazard function implies. Fortunately, the survival function is related to the CDF by
and to the hazard function by
It is therefore possible, in principle, to compute the CDF from nothing but the hazard function. Knowing the CDF, it is possible to compute the inverse of the CDF, and it is this fact which I exploit.
Inverse transform sampling
The probability integral transform (PIT) is a super useful thing to know about. It’s used in multiple statistical methods and is the core of copula theory. I’ve asked people about it in interviews before. Anyway, the PIT says that for any random variable \(X\) with CDF \(F_{X}\), the random variable
is distributed Uniform(0,1). Super simple. If you want to sample from the distribution with CDF \(F_{X}\) and you know how to sample from the uniform distribution, all you need to do is take the inverse transform of your uniform sample! Therefore, if I can get an inverse CDF from my hazard function, then I can sample using inverse transform sampling.
Putting the pieces together
The key steps are as follows:
- Draw a number, \(u\), from the Uniform(0,1) distribution
- Use some numerical solver to solve \(u=F\left(t\right)\)
- The solution, \(t\), from step 2 is drawn from the desired distribution
It is step 2 that’s tricky, of course. All I have is the hazard function, and I need to find the inverse of the CDF. I used a bisection solution strategy to solve the equation in 2. To evaluate the CDF at each step of the bisection search, I used scipy.integrate.quad to numerically integrate the hazard function, then exploited the relationship between cumulative hazard and CDF. The full code is in this gist.
Demonstration
In the code below I sample survival times from the distribution implied by the hazard function
Check it out.
import numpy
from samplers import HazardSampler
# Set a random seed and sample size
numpy.random.seed(1)
m = 1000
# Use this totally crazy hazard function
hazard = lambda t: numpy.exp(numpy.sin(t) - 2.0)
# Sample failure times from the hazard function
sampler = HazardSampler(hazard)
failure_times = numpy.array([sampler.draw() for _ in range(m)])
# Apply some non-informative right censoring, just to demonstrate how it's done
censor_times = numpy.random.uniform(0.0, 25.0, size=m)
y = numpy.minimum(failure_times, censor_times)
c = 1.0 * (censor_times > failure_times
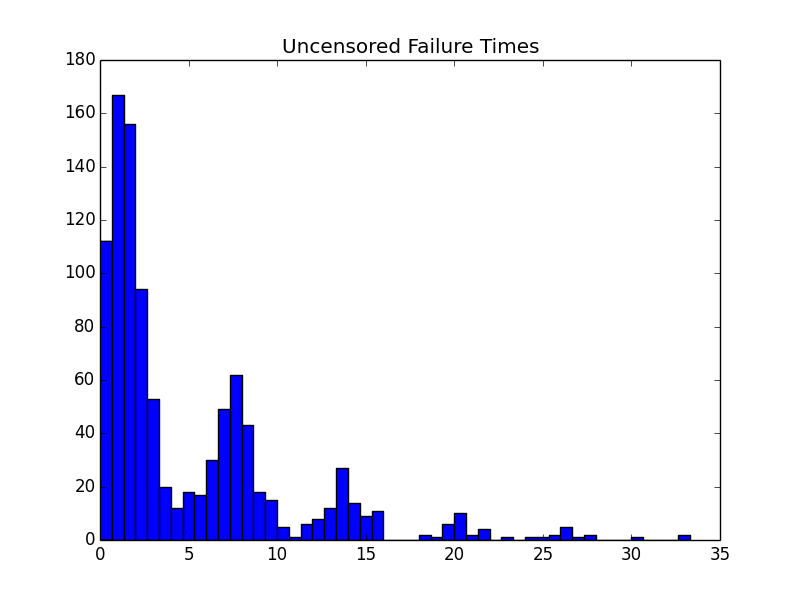
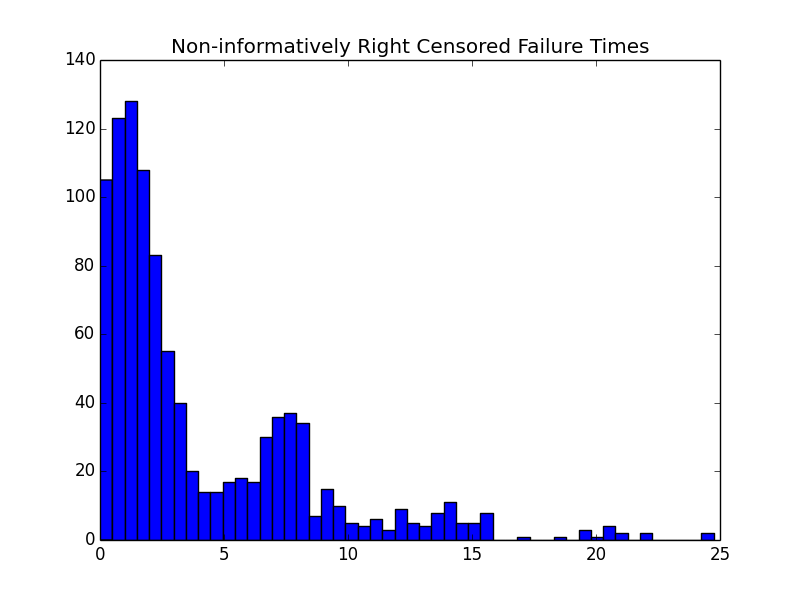
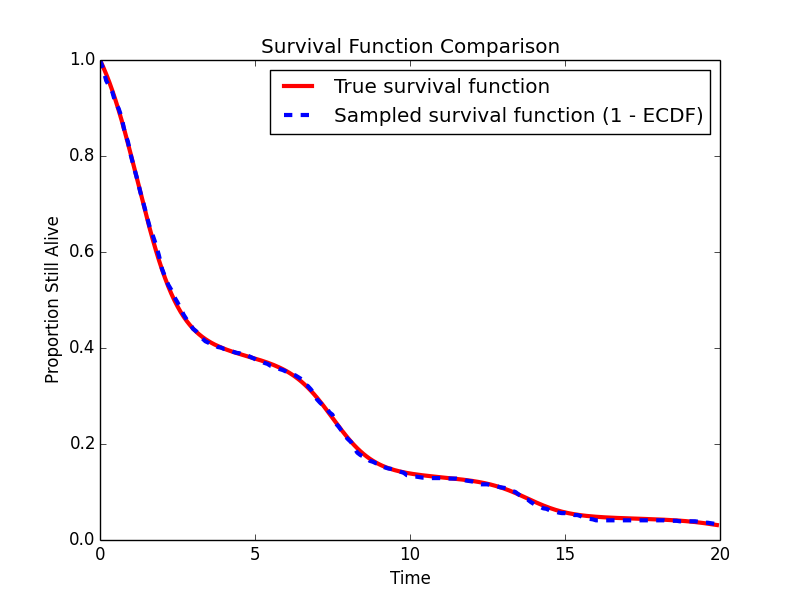
Now let’s make some plots to see how it looks. First I’ll make histograms of the uncensored and censored survival times. Then I’ll compare the true survival function to an estimate based on the uncensored sample.
# Make some plots of the simulated data
from matplotlib import pyplot
from statsmodels.distributions import ECDF
# Plot a histogram of failure times from this hazard function
pyplot.hist(failure_times, bins=50)
pyplot.title('Uncensored Failure Times')
pyplot.savefig('uncensored_hist.png')
pyplot.show()
# Plot a histogram of censored failure times from this hazard function
pyplot.hist(y, bins=50)
pyplot.title('Non-informatively Right Censored Failure Times')
pyplot.savefig('censored_hist.png')
pyplot.show()
# Plot the empirical survival function (based on the censored sample) against the actual survival function
t = numpy.arange(0,20.0,.1)
S = numpy.array([sampler.survival_function(t[i]) for i in range(len(t))])
S_hat = 1.0 - ECDF(failure_times)(t)
pyplot.figure()
pyplot.title('Survival Function Comparison')
pyplot.plot(t, S, 'r', lw=3, label='True survival function')
pyplot.plot(t, S_hat, 'b--', lw=3, label='Sampled survival function (1 - ECDF)')
pyplot.legend()
pyplot.xlabel('Time')
pyplot.ylabel('Proportion Still Alive')
pyplot.savefig('survival_comp.png')
pyplot.show()
The resulting histograms look about how you’d expect for this weird hazard function.
The sample estimated survival function matches well with the actual survival function.
Final thoughts
This algorithm is kind of slow, since it involves repeated numerical integration. Furthermore, my implementation is not as efficient as it could be. For example, I could do most of the numerical integration up front instead of on demand. I also do the root finding in pure Python. But, at least now I can draw samples from any hazard function I want! For my purposes the slowness is not such a big deal, as I only need to simulate data sets to test my hazard regression methods. Once I have the sample, I simply put it in a file and use it as needed. If you wanted to do this as part of some kind of monte carlo algorithm or something, you might need to write a more efficient implementation. I would estimate 100-1000x speedup is possible with a lot of effort.
Follow up
Apparently I should have searched harder, because it looks like there is actually an R package that does almost exactly what I wanted. I haven’t looked in detail, but it appears to also use an inversion-based method and I think handles arbitrary hazard functions.
Transformations and consequences
He knows she tried to be forgiving, but who can just shrug away a guilty lie, a stab in the back? Such a mistake will change a relationship irreversibly, even if we have learned from the mistake and would never repeat it.
—In game text from Braid
Today I want to talk about mistakes. No, not mistakes, really. A mistake is something we regret, something with lingering consequences, like when you work too much on a laptop and get a painful neck spasm that lasts the rest of the week. A mistake is an action that, if we had the chance to go back and try again, we would do differently. But there are some actions that we regret, whose consequences linger painfully, but that we wouldn’t do differently even if we somehow had the chance. In either case we limp along as best we can, trying to compensate for that which is irretrievably lost.
I’m alluding, of course, to the Box-Cox transformation, and, more generally, to all those nonlinear monotonic transformations which may be applied to a response variable in a regression problem to make the regression perform better. These kinds of transformations can sometimes mark the difference between a model that is quite predictive and one that is over fit and not at all predictive on the testing set. The problem, of course, is that once you build your model on the transformed response variable, it becomes difficult to make predications on the original response scale. One can’t simply apply the inverse of the original transformation to the predictions and expect everything to be fine. Everything will not be fine. Today I want to talk about what happens after the nonlinear monotonic transformation. It wasn’t a mistake. It’s just a mess, but we’re in this mess together.
Let’s say we’ve got some response \(y\) and a nonlinear monotonic transformation \(f\left(\right)\). Let’s have \(z=f\left(y\right)\) and say we have some pretty good predictor \(\hat{z}\) of \(E\left(z\right)\). Firstly, what makes this predictor pretty good? How can we compare it to some other predictor, \(\hat{y}\), that we built for \(E\left(y\right)\) on the original scale? It’s a popular practice to use the coefficient of determination, \(R^2\), to assess the predictive power of a regression model, but \(R^2\) is very sensitive to nonlinear transformations. A better idea in this context is to use a rank based measure of predictive power, such as Spearman’s \(\rho\) or Kendall’s \(\tau\). These metrics will not be influenced by any monotonic transformation. I also like to compare \(R^2\) between the training set and a reserved testing set for my regression models. Often I will find extreme overfitting on the original response scale while the model I fit on the transformed response shows good generalization.
So we’ve assessed predictiveness and generalization for our models, and the best one is \(\hat{z}\). Great. That means we have a model for \(E\left(f\left(y\right)\right)\) and we want a model for \(E\left(y\right)\). We know \(f\left(y\right)\), and since it’s monotonic we can presumably find the inverse \(f^{-1}\left(z\right)=y\). However, \(E\left(f\left(y\right)\right)\ne f\left(E\left(y\right)\right)\) in general, so it is also not generally true that \(f^{-1}\left(E\left(f\left(y\right)\right)\right) = E\left(y\right)\). In fact it is usually false. Super false. It turns out that this data transformation problem is similar to another problem about which a group of scientists in La Jolla has recently published a few short articles: risk model calibration. I stumbled upon their publications recently when I was researching the topic of this post [1][2][3]. The problems are essentially identical: given a predictive model with good rank-based performance (area under the ROC curve in the case of classifiers, Spearman’s \(\rho\) or Kendall’s \(tau\) in the case of regression problems with numeric response), find a transformation such that the output of that model accurately predicts the expected value of the quantity of interest. Generally, a monotonic transformation is desired so that the rank-based performance is preserved, but one of the three methods described by the lab in question actually gives a transformation that is not strictly monotonic. I don’t want to describe the methods in detail here. The papers I cited are freely available online. I mostly just want to share a few methods I implemented that are very similar (and were inspired by these scientists’ fine work).
An example
First I’m going to simulate a simple regression problem with a lognormal response distribution.
import numpy
from matplotlib import pyplot
from calibrators import SmoothIso, SmoothMovingAverage, spearman, kendall
numpy.random.seed(0)
# Generate some fake data with a lognormal distribution
m = 10000
n = 10
sigma = 1.0
X = numpy.random.normal(size=(m,n))
beta = 2.0 * numpy.random.binomial(1,.5,size=n) * numpy.random.uniform()
eta = numpy.dot(X, beta)
mu = eta
y = numpy.random.lognormal(mean=mu, sigma=sigma, size=m)
Next, I’m going to fit a linear regression model to the simulated data on the log scale.
# Do a linear regression on the log of the data
z = numpy.log(y)
beta_hat = numpy.linalg.lstsq(X, z)[0]
z_hat = numpy.dot(X, beta_hat)
The goal now is to find a way to go from z_hat back to some estimate of y. Of course we could have just done linear regression on the data scale directly, like this.
# Try doing linear regression directly
beta_hat_direct = numpy.linalg.lstsq(X, y)[0]
y_hat = numpy.dot(X, beta_hat_direct)
# Compare the two models
rho = spearman(y, z_hat)
rho_direct = spearman(y, y_hat)
tau = kendall(y, z_hat)
tau_direct = kendall(y, y_hat)
print 'rho is %f for the log model and %f for the direct model' % (rho, rho_direct)
print 'tau is %f for the log model and %f for the direct model' % (tau, tau_direct)
# rho is 0.802388 for the log model and 0.800836 for the direct model
# tau is 0.606838 for the log model and 0.605232 for the direct model
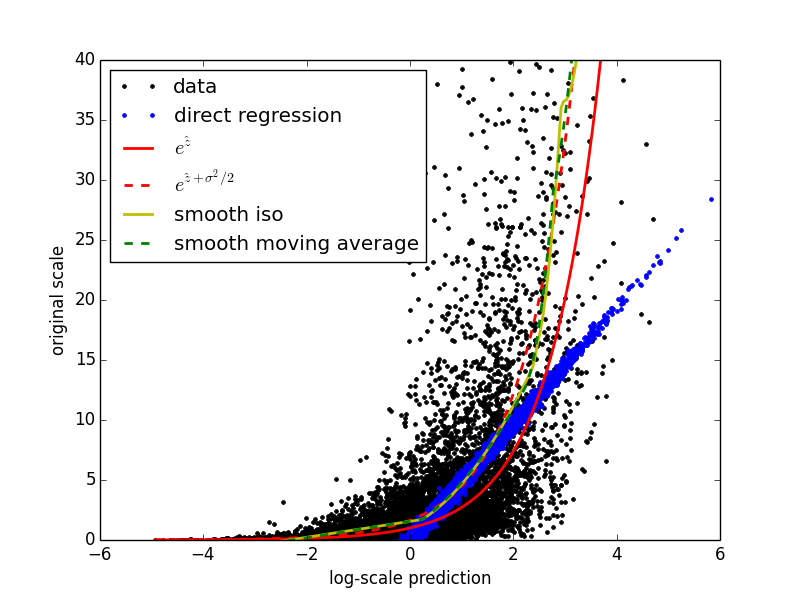
In this case, the difference in rank-based performance between the two models is not significant. I just wanted to show how the comparison might be made. When using more complex nonparametric methods, data scale has a significant effect on generalization ability of the fitted models. With linear regression on this particular problem, overfitting is not really an issue. Now I want to try out some different ways of reversing the log transformation on the predictions. It turns out that for this particular problem, where the data have a known lognormal distribution, the exact right answer is known. That is, it is a provable fact that \(E\left(y\right) = e^{E\left(z\right) + \frac{\sigma^2}{2}}\), where \(\sigma\) is the known scale parameter of the lognormal distribution. I will use this result as a basis for comparison. First, I’m going to try using the obvious and wrong inverse, \(\hat{y} = e^{\hat{z}}\). Next, I’m going to use the two methods I implemented, SmoothIso (based on the idea from [2]) and SmoothMovingAverage (based more loosely on the idea from [1]). Finally, I’ll plot the results together to see how they compare.
# Range for plotting calibration curves
z_range = numpy.arange(z_hat.min(), z_hat.max(), .05)
# Try reversing the log by inversion
y_hat_inv = numpy.exp(z_range)
# Try reversing the log by the actual correct formula
y_hat_correct = numpy.exp(z_range + (sigma**2)/2.0)
# Try reversing the log using SmoothIso
smooth_iso = SmoothIso(max_degree=2).fit(z_hat, y)
y_hat_si = smooth_iso.predict(z_range)
# Try reversing the log using SmoothMovingAverage
moving_average = SmoothMovingAverage(max_degree=2).fit(z_hat, y)
y_hat_sma = moving_average.predict(z_range)
# Plot the different reversal attempts
lw = 2
pyplot.plot(z_hat, y, 'k.', label='data', lw=lw)
pyplot.plot(z_hat, y_hat, 'b.', label='direct regression', lw=lw)
pyplot.plot(z_range, y_hat_inv, 'r', label='$e^{\hat{z}}$', lw=lw)
pyplot.plot(z_range, y_hat_correct, 'r--', label='$e^{\hat{z} + \sigma^{2}/2 }$', lw=lw)
pyplot.plot(z_range, y_hat_si, 'y', label='smooth iso', lw=lw)
pyplot.plot(z_range, y_hat_sma, 'g--', label='smooth moving average', lw=lw)
pyplot.ylim(0,40)
pyplot.legend(loc=0)
pyplot.savefig('example.png', transparent=True)
pyplot.show()
Here is the resulting plot.
Final thoughts
The plot illustrates nicely that simply inverting the original transformation (solid red line) is a very bad idea. On this data set both the calibration methods stick near the correct (dashed red) curve, and I have found them to be effective for real data sets as well. What’s nice about both calibration methods is that they are purely data driven. They will work just as well in situations in which the exact distribution of the data is either not convenient or not known, or even in situations in which the original transformation is unknown. Instead of making distributional assumptions and trying to solve integrals, you can just plug in these calibration methods and most likely end up with a better result.
So, how does all this work? The exact details are beyond the scope of this particular blog entry, but generally speaking SmoothIso works by performing isotonic regression followed by MARS, and SmoothMovingAverage works by training a MARS model on a moving average of the training data. I encourage you to read the articles and check out my implementations. I’m putting all the code used in this post, including the calibrators themselves, in a github repository. I hope you’ll try it.
| [1] | (1, 2) Xiaoqian Jiang, Melanie Osl, Jihoon Kim, and Lucila Ohno-Machado. Calibrating predictive model estimates to support personalized medicine.. Journal of the American Medical Informatics Association, 19(2):263–274, 2011. |
| [2] | (1, 2) Xiaoqian Jiang, Melanie Osl, Jihoon Kim, and Lucila Ohno-Machado. Smooth isotonic regression: a new method to calibrate predictive models.. AMIA Summits Transl Sci Proc. 2011, 2011:16–20, January 2011. |
| [3] | Yuan Wu, Xiaoqian Jiang, Jihoon Kim, and Lucila Ohno-machado. I-spline Smoothing for Calibrating Predictive Models. AMIA Summits Transl Sci Proc. 2012, pages 39–46, 2012. |
Boosting with MARS
Someone wrote me a few months ago asking for advice. He was an R user who wanted to combine the adaboost algorithm with MARS and was starting to look outside the R community. As a recovering (and occasionally relapsing) R user myself, I was only too happy to look into the matter. As it turns out, it’s actually not that hard to do with a combination of scikit-learn and py-earth. I now recount the adventure in detail.
Let it be known that this fine community member was interested in MARS not for regression, as is its usual role, but for classification. This first challenge is easily accomplished using the Pipeline class, as follows.
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from pyearth import Earth
model = Pipeline([('earth',Earth()),('log',LogisticRegression())])
The above construction is equivalent to using the earth package from R with glm=list(family=binomial).
Adaboost requires a classifier that can handle weighted samples. The Earth class satisfies this requirement. LogisticRegression does not, but we can replace it with SGDClassifier using loss=’log’ to get an equivalent Pipeline that can handle sample weights. Or, at least, it seems like it could. As it turns out, though, the Pipeline class doesn’t actually know how to act as a base estimator in AdaBoostClassifier. When you try to fit the resulting model, you get an error.
from sklearn.pipeline import Pipeline
from pyearth import Earth
from sklearn.linear_model.stochastic_gradient import SGDClassifier
from sklearn.datasets import make_classification
from sklearn.ensemble.weight_boosting import AdaBoostClassifier
X, y = make_classification()
classifier = Pipeline([('earth',Earth()),('log',SGDClassifier(loss='log'))])
model = AdaBoostClassifier(base_estimator=classifier)
model.fit(X, y)
This code produces TypeError: base_estimator must be a subclass of ClassifierMixin. You can get to the next error by making a special subclass of Pipeline like so.
from sklearn.pipeline import Pipeline
from pyearth import Earth
from sklearn.linear_model.stochastic_gradient import SGDClassifier
from sklearn.datasets import make_classification
from sklearn.ensemble.weight_boosting import AdaBoostClassifier
from sklearn.base import ClassifierMixin
class ClassifierPipeline(Pipeline, ClassifierMixin):
@property
def classes_(self):
return self.steps[-1][1].classes_
X, y = make_classification()
classifier = ClassifierPipeline([('earth',Earth()),('log',SGDClassifier(loss='log'))])
model = AdaBoostClassifier(base_estimator=classifier)
model.fit(X, y)
Now this code gives ValueError: need more than 1 value to unpack. That’s somewhat more inscrutible. To get around this one you actually have to rewrite part of the Pipeline class itself. I posted a modified Pipeline as a gist. You can patch it in and use it like this.
import pipeline as alt_pipeline
from sklearn.base import ClassifierMixin
from pyearth import Earth
from sklearn.linear_model.stochastic_gradient import SGDClassifier
from sklearn.datasets import make_classification
from sklearn.ensemble.weight_boosting import AdaBoostClassifier
class ClassifierPipeline(alt_pipeline.Pipeline, ClassifierMixin):
@property
def classes_(self):
return self.steps[-1][1].classes_
X, y = make_classification()
classifier = ClassifierPipeline([('earth',Earth()),('log',SGDClassifier(loss='log'))])
model = AdaBoostClassifier(base_estimator=classifier)
model.fit(X, y)
So that’s how you use AdaBoost with MARS in Python.
Introduction to IScala
Python is an amazingly productive glue language. It’s become popular among data scientists over the past several years, partially because of great libraries like numpy, scipy, pandas, scikit-learn, statsmodels, etc., and partially because so much of data science consists simply of gluing things together. There is a part of my life, though, that consists of actually implementing machine learning algorithms. Python does not make that part easy. In order to write efficient numerical code for Python, you need to move the majority of the computation out of Python and into statically typed, compiled code. The best solution I’ve found is Cython, which compiles a Python-like language to C while taking care of the Python C api for you. I wrote py-earth in Cython and am fairly happy with the result. However, Cython is still a (really fantastic) hack. Getting good performance out of Cython code requires knowledge of both C and the internals of Python, and most of the good stuff about Python - passing around functions, object-oriented design, readability - is lost when you start to really optimize. If you want to combine concurrency with objects, you actually have to start passing pointers around.
I guess what I’m saying is I want to branch out a little. I’d like to find a language where I can be productive both as a scientific user and as a scientific developer, something modern, new but not too new, mainstream but with just a bit of an edge. Tall. Anyway, it seems like there are two new languages out there vying for my affection. I chose Scala over Julia for two reasons. Firstly, Scala is a general purpose programming language. While statisticians and academic scientists are very happy to use single purpose tools like R to do their analyses, data scientists need the ability to actually write software and integrate their analyses into larger projects. Secondly, Scala is implemented on the JVM and compatible with Java. That means I can use any Java library from within Scala and use Scala to write map-reduce queries for an Hadoop cluster without using the streaming interface.
So I’m exploring the Scala ecosystem and learning the language (which so far I think is fantastic). My goal is to do some data analyses and implement one or two non-trivial algorithms in Scala. But one step at a time. Today I want to share IScala, which is basically just IPython with a Scala backend. Although I actually rarely use IPython, I know a lot of people do and I suspect that Scala adoption will require the existence of a useful IPython replacement.
Installing
The IScala readme file lists several installation options. The one that worked for me was as follows. First, download the latest tarball and unpack it somewhere. I put it directly in my home directory. Then create a scala profile for ipython:
$ipython profile create scala
[ProfileCreate] Generating default config file: u'/Users/jason/.ipython/profile_scala/ipython_config.py'
[ProfileCreate] Generating default config file: u'/Users/jason/.ipython/profile_scala/ipython_qtconsole_config.py'
[ProfileCreate] Generating default config file: u'/Users/jason/.ipython/profile_scala/ipython_notebook_config.py'
[ProfileCreate] Generating default config file: u'/Users/jason/.ipython/profile_scala/ipython_nbconvert_config.py'
The output above tells you the location of the ipython_config.py file. The next step is to edit ipython_config.py to tell IPython about the IScala kernel, as below:
# Configuration file for ipython.
c = get_config()
# Use the IScala kernel
c.KernelManager.kernel_cmd = ["java", "-jar",
"$ISCALA_PATH/lib/IScala.jar",
"--profile",
"{connection_file}",
"--parent"]
After you get this working, with $ISCALA_PATH replaced by the path to wherever you put the unpacked IScala download, you should be able to run IScala by saying:
$ipython notebook --profile scala
or similarly for console or qtconsole.
Taking it for a spin
I’m going to try generating a random matrix with a standard normal distribution. The first thing I’ll need to do is import breeze. My first attempt failed.
import breeze.linalg._
import breeze.stats.distributions._
<console>:7: error: not found: value breeze
import breeze.linalg._
^
<console>:8: error: not found: value breeze
import breeze.stats.distributions._
^
I needed to tell sbt where to find breeze. It turns out you can use IPython magic to talk to sbt like this.
%resolvers += "ScalaNLP Maven2" at "http://repo.scalanlp.org/repo"
%resolvers += "Scala Tools Snapshots" at "http://scala-tools.org/repo-snapshots/"
%resolvers += "Typesafe Repository" at "http://repo.typesafe.com/typesafe/releases/"
%resolvers += "Sonatype Snapshots" at "https://oss.sonatype.org/content/repositories/snapshots"
%libraryDependencies += "org.scalanlp" %% "breeze" % "0.6-SNAPSHOT"
%update
[info] Resolving org.scalanlp#breeze_2.10;0.6-SNAPSHOT ...
[info] Resolving org.scala-lang#scala-library;2.10.3 ...
[info] Resolving org.scalanlp#breeze-macros_2.10;0.1 ...
[info] Resolving org.scala-lang#scala-reflect;2.10.3 ...
[info] Resolving com.thoughtworks.paranamer#paranamer;2.2 ...
[info] Resolving com.github.fommil.netlib#all;1.1.2 ...
[info] Resolving net.sourceforge.f2j#arpack_combined_all;0.1 ...
[info] Resolving com.github.fommil.netlib#core;1.1.2 ...
[info] Resolving com.github.fommil.netlib#netlib-native_ref-osx-x86_64;1.1 ...
[info] Resolving com.github.fommil.netlib#native_ref-java;1.1 ...
[info] Resolving com.github.fommil#jniloader;1.1 ...
[info] Resolving com.github.fommil.netlib#netlib-native_ref-linux-x86_64;1.1 ...
[info] Resolving com.github.fommil.netlib#netlib-native_ref-linux-i686;1.1 ...
[info] Resolving com.github.fommil.netlib#netlib-native_ref-win-x86_64;1.1 ...
[info] Resolving com.github.fommil.netlib#netlib-native_ref-win-i686;1.1 ...
[info] Resolving com.github.fommil.netlib#netlib-native_ref-linux-armhf;1.1 ...
[info] Resolving com.github.fommil.netlib#netlib-native_system-osx-x86_64;1.1 ...
[info] Resolving com.github.fommil.netlib#native_system-java;1.1 ...
[info] Resolving com.github.fommil.netlib#netlib-native_system-linux-x86_64;1.1 ...
[info] Resolving com.github.fommil.netlib#netlib-native_system-linux-i686;1.1 ...
[info] Resolving com.github.fommil.netlib#netlib-native_system-linux-armhf;1.1 ...
[info] Resolving com.github.fommil.netlib#netlib-native_system-win-x86_64;1.1 ...
[info] Resolving com.github.fommil.netlib#netlib-native_system-win-i686;1.1 ...
[info] Resolving org.scalanlp#lpsolve;5.5.2-SNAPSHOT ...
[info] Resolving net.sf.opencsv#opencsv;2.3 ...
[info] Resolving com.github.rwl#jtransforms;2.4.0 ...
[info] Resolving junit#junit;4.8.2 ...
[info] Resolving org.apache.commons#commons-math3;3.2 ...
[info] Resolving com.typesafe#scalalogging-slf4j_2.10;1.0.1 ...
[info] Resolving org.slf4j#slf4j-api;1.7.2 ...
import breeze.linalg._
import breeze.stats.distributions._
That worked! I can now generate my random matrix like this:
val x = DenseMatrix.fill(10,10)(Gaussian(0,1).draw())
0.4695170376110142 0.5086639312405534 ... (10 total)
0.2604624080687952 -0.03678938632256435 ...
-1.0528337756159565 0.10082649287241126 ...
-0.550492849679171 -0.5761878622563654 ...
-0.9817603551889219 0.7958446618784706 ...
-1.0001995322763473 -1.2424889465651479 ...
-0.5879313146878662 1.206569217055404 ...
1.890300548243616 -0.30273380341887257 ...
0.24792587873136573 -0.04329745764599858 ...
1.5057194826425122 0.9516921598743895 ...
Final thoughts
So IScala is up and running. There doesn’t yet appear to be any support for displaying plots in the notebook, and it is a little annoying that I have to %update to add new dependencies (which causes the Scala process to restart and all existing objects to be lost from memory). However, IScala is a new project and these are minor issues. During the process I discovered something disconcerting about the Scala ecosystem, however. There is not currently a Scala equivalent of numpy. That is, there is no basic structure that everyone agrees is the standard backend array type. Instead, there are several competing packages (of which breeze is just one) that accomplish this extremely basic function. I need to decide which one I want to develop on.
Blogstart
Once in a great while a new blog is born, and today these rusty tubes are graced with a sparkling new presence. It’s a little rough right now, but greatness can grow from meek beginnings. Let us take a moment to remember some of the great weblogs of the past, whose unfathomable heights this humble site may hope one day to spy on the horizon. Pythonic Perambulations, While My MCMC Gently Samples, and all the rest, may I follow in your sizable footsteps. This blog will be much in the spirit of these gentle giants. It will concern my work and particularly my Python code. It will contain short pieces of opinion, medium length demonstrations of technology, and longer analyses of data. It will not be limited to Python or even to programming and statistics, but will tend to concern those topics more than any other. At least that is my intention.
Blog rules [1]
Every blog needs rules. Here are some.
- Trust no one.
- Posts occur at least once per month.
- Nothing is final. If you want to see revision history, the blog is hosted on github.
Blog implementation
This blog, at least at the moment, is constructed using the Tinkerer static blogging framework. Why Tinkerer you ask? When choosing a static blogging framework I considered the following options: Octopress, Jekyll, Hyde, Pelican, and Tinkerer. I ruled out Octopress and Jekyll easily enough. Although they’re both popular, they’re not Python and it would therefore be hard for me to read and understand the source code should the unthinkable occur. Of the three remaining, I chose Tinkerer because it is based on Sphinx. Sphinx is a mature and well supported Python tool for generating documentation. Its main selling points for me are the easy support for math, syntax-highlighted code, bibtex, footnotes, and basically every other imaginable feature of a document via an impressive collection of plugins. The downside of Tinkerer is that its relatively small userbase has produced very few nice looking themes. However, I’ve decided theming is a secondary consideration for now. Perhaps I can help to remedy the situation in the near future.
| [1] | As with any ordered set of rules, the zeroeth rule is that there are no rules. |